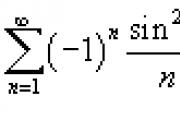Знакопеременные ряды. Сходимость знакопеременных рядов Знакопеременные ряды. Абсолютная и условная сходимость ряда

Числовой ряд, содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называется знакопеременным.

Абсолютная и условная сходимость

Ряд называется абсолютно сходящимся, если ряд также сходится.

Если ряд сходится абсолютно, то он является сходящимся (в обычном смысле). Обратное утверждение неверно.

Ряд называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.

Исследовать на сходимость ряд .

Применим достаточный признак Лейбница для знакочередующихся рядов. Получаем

поскольку . Следовательно, данный ряд сходится.

38. Знакочередующиеся ряды. Признак Лейбница.

Частным случаем знакопеременного ряда является знакочередующийся ряд, то есть такой ряд, в котором последовательные члены имеют противоположные знаки.

Признак Лейбница

Для знакочередующихся рядом действует достаточный признак сходимости Лейбница.

Пусть {an} является числовой последовательностью, такой, что

1. an+1 < an для всех n;

Тогда знакочередующиеся ряды исходятся.

39. Функциональные ряды. Степенные ряды. Радиус сходимости. Интервал сходимости.

Понятие функционального ряда и степенного ряда

Обычный числовой ряд, вспоминаем, состоит из чисел:

Все члены ряда –это ЧИСЛА.

Функциональный же ряд состоит из ФУНКЦИЙ:

В общий член рядапомимо многочленов, факториалов и других подарков непременно входит буковка «икс». Выглядит это, например, так:

Как и числовой ряд, любой функциональный ряд можно расписать в развернутом виде:

Как видите, все члены функционального ряда это функции.

Наиболее популярной разновидностью функционального ряда является степенной ряд.

Определение:

Степенной ряд – это ряд, в общий член которого входят целые положительные степени независимой переменной.

Упрощенно степенной ряд во многих учебниках записывают так: , где– это старая знакомая «начинка» числовых рядов (многочлены, степени, факториалы, зависящие только от «эн»). Простейший пример:

Посмотрим на это разложение и еще раз осмыслим определение: члены степенного ряда содержат «иксы» в целых положительных (натуральных) степенях.

Очень часто степенной ряд можно встретить в следующих «модификациях»: илигде а – константа. Например:

Строго говоря, упрощенные записи степенного ряда,илине совсем корректны. В показателе степени вместо одинокой буквы «эн» может располагаться более сложное выражение, например:

Или такой степенной ряд:

Лишь бы показатели степеней при «иксАх» были натуральными.

Сходимость степенного ряда .

Интервал сходимости, радиус сходимости и область сходимости

Не нужно пугаться такого обилия терминов, они идут «рядом друг с другом» и не представляют особых сложностей для понимания. Лучше выберем какой-нибудь простой подопытный ряд и сразу начнём разбираться.

Прошу любить и жаловать степенной ряд Переменная может принимать любое действительное значение от «минус бесконечности» до «плюс бесконечности». Подставим в общий член ряда несколько произвольных значений «икс»:

Если х=1,то

Если х=-1,то

Если х=3,то

Если х=-0,2, то

Очевидно, что, подставляя в то или иное значение «икс», мы получаем различные числовые ряды. Некоторые числовые ряды будут сходиться, а некоторые расходиться. И наша задача найти множество значений «икс», при котором степенной рядбудет сходиться. Такое множество и называется областью сходимости ряда.

Для любого степенного ряда (временно отвлекаемся от конкретного примера) возможны три случая:

1) Степенной ряд сходится абсолютно на некотором интервале . Иными словами, если мы выбираем любое значение «икс» из интервалаи подставляем его в общий член степенного ряда, то у нас получается абсолютно сходящийся числовой ряд. Такой интервал и называется интервалом сходимости степенного ряда.

Радиус сходимости, если совсем просто, это половина длины интервала сходимости:

Геометрически ситуация выглядит так:

В данном случае, интервал сходимости ряда: радиус сходимости ряда:

Рассмотрим ряды, члены которых имеют произвольные знаки, такие ряды будем называть знакопеременными (заметим, что в математической литературе термины знакопеременный и знакочередующийся ряд – о таких рядах речь пойдет позже – означают одно и то же; но мы здесь приняли терминологию, используемую Пискуновым Н.С. в его «Дифференциальном и интегральном исчислении» только для сокращения записи: вместо слов «ряд, члены которого имеют произвольные знаки» будем говорить «знакопеременные ряды»). Если заданный ряд имеет только конечное число отрицательных членов, то, отбросив их, можно свести дело к исследованию ряда с положительными членами. То же касается ряда, в котором только конечное число положительных членов. Поэтому будем заведомо предполагать, что среди членов ряда есть бесконечное количество как положительных, так и отрицательных членов.

Справедлива следующая теорема

Теорема 30. 8. (признак абсолютной сходимости)

Пусть дан ряд с членами произвольных знаков. Если сходится ряд

составленный из абсолютных величин его членов, то сходится и данный ряд. При этом .

Определение 30.4. Если ряд сходится и сходится ряд , то ряд называется абсолютно сходящимся . Если ряд сходится, а ряд расходится, то ряд называется условно (не абсолютно) сходящимся .

Для выяснения абсолютной сходимости заданного ряда к ряду из его модулей могут быть применены признаки, рассмотренные нами в предыдущем пункте. Но нужно быть осторожным с признаками расходимости: если ряд из модулей расходится, то исходный ряд может и сходиться (условно). Исключение составляют лишь признак Даламбера и радикальный признак Коши, так как когда эти признаки констатируют расходимость ряда , то это означает, что , но тогда и , что означает расходимость ряда .

Сформулируем эти признаки применительно к знакопеременному ряду

Признак Даламбера. , то

при d < 1 ряд сходится абсолютно,

при d > 1 ряд расходится,

при d =1 нужны дополнительные исследования.

Признак Коши радикальный. Если для знакопеременного ряда существует , то

при K < 1 ряд сходится абсолютно,

при K > 1 ряд расходится,

при K = 1 требуются дополнительные исследования

Пример. Исследуем сходимость ряда . Применим к нему признак Коши: – ряд сходится абсолютно.

Среди знакопеременных рядов особую роль играют так называемые знакочередующиеся ряды . Знакочередующимся рядом называют ряд, члены которого поочередно имеют то положительный, то отрицательный знаки (см предыдущий пример). Такой ряд обычно записывают в виде

при этом предполагается, то все а п > 0.

Для знакочередующихся рядов имеет место

Теорема 30.9. (Теорема Лейбница)

Если члены знакочередующегося ряда убывают по абсолютной величине, т.е."п | a n | >| a n +1 |, и , то ряд сходится. При этом сумма ряда по абсолютной величине не превосходит модуля первого члена ряда, т.е. и имеет тот же знак, что и первый член ряда.

Ряд, удовлетворяющий условиям теоремы Лейбница, называют рядом лейбницевского типа.

Пример . Рассмотрим сходимость ряда . Проверим выполнение условий Теоремы 5.9.: | a n | >| a n +1 |, действительно, > "п ³1, а также , значит, ряд сходится. А так как ряд из абсолютных величин этого ряда есть расходящийся гармонический ряд , то исходный ряд сходится условно.

Замечание. Так как любой остаток ряда лейбницевского типа есть также ряд лейбницевского типа, то в случае сходимости ряда, остаток ряда по абсолютной величине не превосходит модуля своего первого члена:

| R n | = |S – S n | £ |a n +1 |.

Это удобно использовать для оценки точности приближенного вычисления суммы данного ряда.

Своим внеочередным появлением данный раздел обязан многим и многим авторам, читая труды которых так и хотелось запустить оными трудами в самих писателей. Собственно, я планировал выложить данную тему полностью лишь по мере её окончательной готовности, однако ввиду слишком большого количества вопросов по ней, изложу некоторые моменты сейчас. Впоследствии материал будет дополнен и расширен. Начнём с определений.

Ряд вида $\sum\limits_{n=1}^{\infty}(-1)^{n+1}u_n$, где $u_n>0$, называется знакочередующимся.

Знаки членов знакочередующегося ряда строго чередуются:

$$ \sum\limits_{n=1}^{\infty}(-1)^{n+1}u_n=u_1-u_2+u_3-u_4+u_5-u_6+u_7-u_8+\ldots $$

Например, $1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\ldots$ - знакочередующийся ряд. Бывает, что строгое чередование знаков начинается не с первого элемента, однако для исследования на сходимость это несущественно.

Почему чередование знаков не с первого элемента является несущественным? показать\скрыть

Дело в том, что среди свойств числовых рядов есть утверждение, которое позволяет нам отбрасывать "лишние" члены ряда. Вот это свойство:

Ряд $\sum\limits_{n=1}^{\infty}u_n$ сходится тогда и только тогда, когда сходится любой из его остатков $r_n=\sum\limits_{k=n+1}^{\infty}u_k$. Отсюда следует, что отбрасывание или добавление к некоторому ряду конечного количества членов не изменяет сходимости ряда.

Пусть нам задан некий знакочередующийся ряд $\sum\limits_{n=1}^{\infty}(-1)^{n+1}u_n$, и пусть для этого ряда выполнено первое условие признака Лейбница, т.е. $\lim_{n\to{\infty}}u_n=0$. Однако второе условие, т.е. $u_n≥u_{n+1}$, выполняется начиная с некоего номера $n_0\in{N}$. Если $n_0=1$, то мы получаем обычную формулировку второго условия признака Лейбница, посему ряд $\sum\limits_{n=1}^{\infty}(-1)^{n+1}u_n$ будет сходиться. Если же $n_0>1$, то разобьём ряд $\sum\limits_{n=1}^{\infty}(-1)^{n+1}u_n$ на две части. В первую часть выделим все те элементы, номера которых меньше $n_0$:

$$ \sum\limits_{n=1}^{\infty}(-1)^{n+1}u_n=\sum\limits_{n=1}^{n_0-1}(-1)^{n+1}u_n+\sum\limits_{n=n_0}^{\infty}(-1)^{n+1}u_n $$

Для ряда $\sum\limits_{n=n_0}^{\infty}(-1)^{n+1}u_n$ выполнены оба условия признака Лейбница, поэтому ряд $\sum\limits_{n=n_0}^{\infty}(-1)^{n+1}u_n$ сходится. Так как сходится остаток, то будет сходиться и исходный ряд $\sum\limits_{n=1}^{\infty}(-1)^{n+1}u_n$.

Таким образом, совершенно неважно, выполнено ли второе условие признака Лейбница, начиная с первого, или же с тысячного элемента - ряд всё равно будет сходиться.

Отмечу, что признак Лейбница является достаточным, но не необходимым условием сходимости знакочередующихся рядов. Иными словами, выполнение условий признака Лейбница гарантирует сходимость ряда, но невыполнение оных условий не гарантирует ни сходимости, ни расходимости. Разумеется, невыполнение первого условия, т.е. случай $\lim_{n\to{\infty}}u_n\neq{0}$, означает расходимость ряда $\sum\limits_{n=n_0}^{\infty}(-1)^{n+1}u_n$, однако невыполнение второго условия может произойти как для сходящегося, так и расходящегося ряда.

Так как знакочередующиеся ряды частенько встречаются в стандартных типовых расчётах, то я составил схему, по которой можно исследовать на сходимость стандартный знакочередующийся ряд.

Разумеется, можно напрямую применять признак Лейбница, минуя проверку сходимости ряда из модулей. Однако для стандартных учебных примеров проверка ряда из модулей необходима, так как большинство авторов типовых расчетов требуют не просто выяснить, сходится ряд или нет, а определить характер сходимости (условная или абсолютная). Перейдем к примерам.

Пример №1

Исследовать ряд $\sum\limits_{n=1}^{\infty}(-1)^{n+1}\frac{4n-1}{n^2+3n}$ на сходимость.

Для начала выясним, действительно ли данный ряд знакочередующийся. Так как $n≥1$, то $4n-1≥3>0$ и $n^2+3n≥4>0$, т.е. при всех $n\in{N}$ имеем $\frac{4n-1}{n^2+3n}>0$. Таким образом, заданный ряд имеет вид $\sum\limits_{n=1}^{\infty}(-1)^{n+1}u_n$, где $u_n=\frac{4n-1}{n^2+3n}>0$, т.е. рассматриваемый ряд - знакочередующийся.

Обычно такая проверка делается устно, однако пропускать её крайне нежелательно: ошибки в типовых расчётах нередки. Часто бывает, что знаки членов заданного ряда начинают чередоваться не с первого члена ряда. В этом случае можно отбросить "мешающие" члены ряда и исследовать сходимость остатка (см. примечание в начале этой страницы).

Итак, нам задан знакочередующийся ряд. Будем следовать вышеприведённой . Для начала составим ряд из модулей членов данного ряда:

$$ \sum\limits_{n=1}^{\infty}\left|(-1)^{n+1}\frac{4n-1}{n^2+3n}\right| =\sum\limits_{n=1}^{\infty}\frac{4n-1}{n^2+3n} $$

Проверим, сходится ли составленный ряд из модулей. Применим признак сравнения . Так как при всех $n\in{N}$ имеем $4n-1=3n+n-1≥3n$ и $n^2+3n≤n^2+3n^2=4n^2$, то:

$$ \frac{4n-1}{n^2+3n}≥ \frac{3n}{4n^2}=\frac{3}{4}\cdot\frac{1}{n} $$

Гармонический ряд $\sum\limits_{n=1}^{\infty}\frac{1}{n}$ расходится, поэтому будет расходиться и ряд $\sum\limits_{n=1}^{\infty}\left(\frac{3}{4}\cdot\frac{1}{n}\right)$. Следовательно, согласно признаку сравнения ряд $\sum\limits_{n=1}^{\infty}\frac{4n-1}{n^2+3n}$ расходится. Обозначим $u_n=\frac{4n-1}{n^2+3n}$ и проверим, выполнены ли условия признака Лейбница для исходного знакочередующегося ряда. Найдём $\lim_{n\to{\infty}}u_n$:

$$ \lim_{n\to{\infty}}u_n =\lim_{n\to{\infty}}\frac{4n-1}{n^2+3n} =\lim_{n\to{\infty}}\frac{\frac{4}{n}-\frac{1}{n^2}}{1+\frac{3}{n}} =0. $$

Первое условие признака Лейбница выполнено. Теперь нужно выяснить, выполнено ли неравенство $u_n≥u_{n+1}$. Немалое количество авторов предпочитает записать несколько первых членов ряда, а затем сделать вывод, что неравенство $u_n≥u_{n+1}$ выполнено.

Иными словами, это "доказательство" для данного ряда имело бы такой вид: $\frac{2}{3}≤\frac{5}{8}≤\frac{8}{15}≤\ldots$. После сравнения нескольких первых членов делается вывод: для остальных членов неравенство сохранится, каждый последующий будет не более предыдущего. Откуда взялся этот "метод доказательства" я не знаю, но он ошибочен. Например, для последовательности $v_n=\frac{10^n}{n!}$ получим такие первые члены: $v_1=10$, $v_2=50$, $v_3=\frac{500}{3}$, $v_4=\frac{1250}{3}$. Как видите, они возрастают, т.е., если ограничиться сравнением нескольких первых членов, то можно сделать вывод, что $v_{n+1}>v_n$ для всех $n\in{N}$. Однако такой вывод будет категорически неверным, так как начиная с $n=10$ элементы последовательности будут убывать.

Как же доказать неравенство $u_n≥u_{n+1}$? В общем случае для этого есть несколько способов. Самый простой в нашем случае - рассмотреть разность $u_n-u_{n+1}$ и выяснить её знак. В следующем примере рассмотрим иной способ: посредством доказательства убывания соответствующей функции.

$$ u_n-u_{n+1} =\frac{4n-1}{n^2+3n}-\frac{4(n+1)-1}{(n+1)^2+3(n+1)} =\frac{4n-1}{n^2+3n}-\frac{4n+3}{n^2+5n+4}=\\ =\frac{(4n-1)\cdot\left(n^2+5n+4\right)-\left(n^2+3n\right)\cdot(4n+3)}{\left(n^2+3n\right)\cdot\left(n^2+5n+4\right)} =\frac{4n^2+2n-4}{\left(n^2+3n\right)\cdot\left(n^2+5n+4\right)}. $$

Так как $n≥1$, то $4n^2-4≥0$, откуда имеем $4n^2+2n-4>0$, т.е. $u_n-u_{n+1}>0$, $u_n>u_{n+1}$. Бывает, конечно, что неравенство $u_n≥u_{n+1}$ выполняется не с первого члена ряда, однако это несущественно (см. в начале страницы).

Таким образом, оба условия признака Лейбница выполнены. Так как при этом ряд $\sum\limits_{n=1}^{\infty}\left|(-1)^{n+1}\frac{4n-1}{n^2+3n}\right|$ расходится, то ряд $\sum\limits_{n=1}^{\infty}(-1)^{n+1}\frac{4n-1}{n^2+3n}$ сходится условно.

Ответ : ряд сходится условно.

Пример №2

Исследовать ряд $\sum\limits_{n=1}^{\infty}(-1)^{n+1}\frac{5n-4}{\sqrt{2n^3-1}}$ на сходимость.

Для начала рассмотрим выражение $\frac{5n-4}{\sqrt{2n^3-1}}$. Стоит произвести небольшую проверку корректности условия. Дело в том, что очень часто в условиях стандартных типовых расчётов можно встретить ошибки, когда подкоренное выражение является отрицательным, или же в знаменателе при некоторых значениях $n$ появляется ноль.

Дабы избежать таких неприятностей, произведём простенькое предварительное исследование. Так как при $n≥1$ имеем $2n^3≥2$, то $2n^3-1≥1$, т.е. выражение под корнем не может быть отрицательным или равняться нулю. Следовательно, условие вполне корректно. Выражение $\frac{5n-4}{\sqrt{2n^3-1}}$ определено при всех $n≥1$.

Добавлю, что при $n≥1$ верно неравенство $\frac{5n-4}{\sqrt{2n^3-1}}>0$, т.е. нам задан знакочередующийся ряд. Будем исследовать его согласно вышеприведённой . Для начала составим ряд из модулей членов данного ряда:

$$ \sum\limits_{n=1}^{\infty}\left|(-1)^{n+1}\frac{5n-4}{\sqrt{2n^3-1}}\right| =\sum\limits_{n=1}^{\infty}\frac{5n-4}{\sqrt{2n^3-1}} $$

Проверим, сходится ли ряд, составленный из модулей членов заданного ряда. Применим признак сравнения . В решении предыдущего примера мы применяли первый признак сравнения. Здесь же, сугубо для разнообразия, применим второй признак сравнения (признак сравнения в предельной форме). Сравним ряд $\sum\limits_{n=1}^{\infty}\frac{5n-4}{\sqrt{2n^3-1}}$ с расходящимся рядом $\sum\limits_{n=1}^{\infty}\frac{1}{\sqrt{n}}$:

$$ \lim_{n\to\infty}\frac{\frac{5n-4}{\sqrt{2n^3-1}}}{\frac{1}{\sqrt{n}}} =\lim_{n\to\infty}\frac{5n\sqrt{n}-4\sqrt{n}}{\sqrt{2n^3-1}} =\lim_{n\to\infty}\frac{\frac{5n\sqrt{n}}{n\sqrt{n}}-\frac{4\sqrt{n}}{n\sqrt{n}}}{\sqrt{\frac{2n^3-1}{n^3}}} \lim_{n\to\infty}\frac{5-\frac{4}{n}}{\sqrt{2-\frac{1}{n^3}}} =\frac{5}{\sqrt{2}}. $$

Так как $\frac{5}{\sqrt{2}}\neq{0}$ и $\frac{5}{\sqrt{2}}\neq\infty$, то одновременно с рядом $\sum\limits_{n=1}^{\infty}\frac{1}{\sqrt{n}}$ будет расходиться и ряд $\sum\limits_{n=1}^{\infty}\frac{5n-4}{\sqrt{2n^3-1}}$.

Итак, абсолютной сходимости заданный знакочередующийся ряд не имеет. Обозначим $u_n=\frac{5n-4}{\sqrt{2n^3-1}}$ и проверим, выполнены ли условия признака Лейбница. Найдём $\lim_{n\to{\infty}}u_n$:

$$ \lim_{n\to{\infty}}u_n =\lim_{n\to{\infty}}\frac{5n-4}{\sqrt{2n^3-1}} =\lim_{n\to{\infty}}\frac{\frac{5n}{n^{\frac{3}{2}}}-\frac{4}{n^{\frac{3}{2}}}}{\sqrt{\frac{2n^3-1}{n^3}}} =\lim_{n\to{\infty}}\frac{\frac{5}{\sqrt{n}}-\frac{4}{n^{\frac{3}{2}}}}{\sqrt{2-\frac{1}{n^3}}} =0. $$

Первое условие признака Лейбница выполнено. Теперь нужно выяснить, выполнено ли неравенство $u_n≥u_{n+1}$. В прошлом примере мы рассмотрели один из способов доказательства этого неравенства: посредством выяснения знака разности $u_n-u_{n+1}$. В этот раз обратимся к иному способу: вместо $u_n=\frac{5n-4}{\sqrt{2n^3-1}}$ рассмотрим функцию $y(x)=\frac{5x-4}{\sqrt{2x^3-1}}$ при условии $x≥1$. Отмечу, что поведение данной функции при условии $x<1$ нам совершенно безразлично.

Наша цель состоит в том, чтобы доказать невозрастание (или убывание) функции $y(x)$. Если мы докажем, что функция $y(x)$ является невозрастающей, то для всех значений $x_2>x_1$ будем иметь $y(x_1)≥y(x_2)$. Полагая $x_1=n$ и $x_2=n+1$ получим, что из неравенства $n+1>n$ последует истинность неравенства $y(n)≥y(n+1)$. Так как $y(n)=u_n$, то неравенство $y(n)≥y(n+1)$ есть то же самое, что и $u_{n}≥u_{n+1}$.

Если же мы покажем, что $y(x)$ - убывающая функция, то из неравенства $n+1>n$ последует истинность неравенства $y(n)>y(n+1)$, т.е. $u_{n}>u_{n+1}$.

Найдём производную $y"(x)$ и выясним её знак для соответствующих значений $x$.

$$ y"(x)=\frac{(5x-4)"\cdot\sqrt{2x^3-1}-(5x-4)\cdot\left(\sqrt{2x^3-1}\right)"}{\left(\sqrt{2x^3-1}\right)^2} =\frac{5\cdot\sqrt{2x^3-1}-(5x-4)\cdot\frac{1}{2\sqrt{2x^3-1}}\cdot{6x^2}}{2x^3-1}=\\ =\frac{5\cdot\left(2x^3-1\right)-(5x-4)\cdot{3x^2}}{\left(2x^3-1\right)^{\frac{3}{2}}} =\frac{-5x^3+12x^2-5}{\left(2x^3-1\right)^{\frac{3}{2}}} $$

Полагаю, очевидно, что при достаточно больших положительных значениях $x≥1$ многочлен в знаменателе будет меньше нуля, т.е. $-5x^3+12x^2-5<0$. Эту "очевидность" несложно обосновать формально - если вспомнить курс алгебры. Дело в том, что согласно лемме о модуле старшего члена, при достаточно больших значениях $|x|$ знак многочлена совпадает с знаком его старшего члена. Адаптируясь к нашей задаче получаем, что существует такое число $c≥1$, то для всех $x≥c$ будет верным неравенство $-5x^3+12x^2-5<0$. В принципе, существования такого числа $c$ уже вполне достаточно для дальнейшего решения задачи.

Однако давайте подойдём к вопросу менее формально. Дабы не привлекать лишних лемм из алгебры, просто грубо оценим значение выражения $-5x^3+12x^2-5$. Учтём $-5x^3+12x^2-5=x^2(-5x+12)-5$. При $x≥3$ имеем $-5x+12<0$, посему $x^2(-5x+12)-5<0$.

Таким образом, при $x≥3$ имеем $y"(x)<0$, т.е. функция $y(x)$ убывает. А это, в свою очередь, означает, что при $n≥3$ верно неравенство $u_n>u_{n+1}$, т.е. второе условие признака Лейбница выполнено. Разумеется, мы показали выполнение второго условия не с $n=1$, а с $n=3$, но это несущественно (см. в начале страницы).

Таким образом, оба условия признака Лейбница выполнены. Так как при этом ряд $\sum\limits_{n=1}^{\infty}\left|(-1)^{n+1}\frac{5n-4}{\sqrt{2n^3-1}}\right|$ расходится, то ряд $\sum\limits_{n=1}^{\infty}(-1)^{n+1}\frac{4n-1}{n^2+3n}$ сходится условно.

Ответ : ряд сходится условно.

Пример №3

Исследовать ряд $\sum\limits_{n=1}^{\infty}(-1)^{n+1}\frac{3n+4}{2^n}$ на сходимость.

Данный пример не представляет большого интереса, поэтому я распишу его коротко. Нам задан знакочередующийся ряд, который вновь станем исследовать по . Составим ряд из модулей членов данного ряда:

$$ \sum\limits_{n=1}^{\infty}\left|(-1)^{n+1}\frac{3n+4}{2^n}\right| =\sum\limits_{n=1}^{\infty}\frac{3n+4}{2^n} $$

Применим признак Д"Аламбера . Обозначая $u_n=\frac{3n+4}{2^n}$, получим $u_{n+1}=\frac{3n+7}{2^{n+1}}$.

$$ \lim_{n\to\infty}\frac{u_{n+1}}{u_{n}} =\lim_{n\to\infty}\frac{\frac{3n+7}{2^{n+1}}}{\frac{3n+4}{2^n}} =\frac{1}{2}\lim_{n\to\infty}\frac{3n+7}{3n+4} =\frac{1}{2}\lim_{n\to\infty}\frac{3+\frac{7}{n}}{3+\frac{4}{n}} =\frac{1}{2}\cdot{1}=\frac{1}{2}. $$

Так как $\frac{1}{2}<1$, то согласно признаку Д"Аламбера ряд $\sum\limits_{n=1}^{\infty}\frac{3n+4}{2^n}$ сходится. Из сходимости ряда $\sum\limits_{n=1}^{\infty}\left|(-1)^{n+1}\frac{3n+4}{2^n}\right|$, что ряд $\sum\limits_{n=1}^{\infty}(-1)^{n+1}\frac{3n+4}{2^n}$ сходится, причём сходится абсолютно.

Отмечу, что для решения заданного примера нам не потребовался признак Лейбница. Именно поэтому удобно сперва проверить сходимость ряда из модулей, а потом уже, при необходимости, исследовать сходимость исходного знакочередующегося ряда.

Ответ : ряд сходится абсолютно.

До сих пор мы изучали только ряды, все члены которых были положительными . Теперь мы перейдем к рассмотрению рядов, содержащих как положительные, так и отрицательные члены. Такие ряды называются знакопеременными.

В качестве примера знакопеременного ряда приведем ряд

Изучение знакопеременных рядов мы начнем с частного случая, так называемых знакочередующихся рядов, т. е. рядов, в которых за каждым положительным членом следует отрицательный и за каждым отрицательным членом следует положительный.

Обозначая через - абсолютные величины членов ряда и считая, что первый член положителен, знакочередующийся ряд запишем следующим образом:

Для знакочередующихся рядов имеет место достаточный признак сходимости Лейбница.

Признак Лейбница. Если в знакочередующемся ряде (34) абсолютные величины членов убывают:

и общий член ряда стремится к нулю: , то ряд сходится и его сумма не превосходит первого члена ряда.

Доказательство. Рассмотрим частичную сумму четного числа членов ряда

Сгруппируем члены попарно:

Так как по условию абсолютные величины членов ряда убывают, то все разности в скобках положительны и, следовательно, сумма положительна и возрастает при увеличении .

Запишем теперь группируя члены иным образом:

Сумма в квадратных скобках будет также положительной. Поэтому для любого значения . Таким образом, последовательность четных частичных сумм возрастает с увеличением , оставаясь при этом ограниченной. Следовательно, имеет предел

При этом, так как то ясно, что Рассмотрим теперь сумму нечетного числа членов:

При имеем

так как по условию и, следовательно, .

Таким образом, частичные суммы как четного, так и нечетного числа членов имеют общий предел S. Это означает, что вообще , т. е. ряд сходится. При этом, как видно из доказательства, сумма ряда S не превосходит первого члена ряда.

Пример 1. Исследовать, сходится или расходится ряд

Решение. Этот ряд удовлетворяет условиям признака Лейбница:

Следовательно, ряд сходится.

Перейдем теперь к рассмотрению общего случая знакопеременного ряда. Будем предполагать, что в ряде

числа могут быть как положительными, так и отрицательными.

Для таких рядов имеет место следующий достаточный признак сходимости знакопеременного ряда.

Теорема. Если для знакопеременного ряда

сходится ряд, составленный из абсолютных величин его членов

то данный знакопеременный ряд также сходится.

Доказательство. Рассмотрим вспомогательный ряд, составленный из членов рядов (37) и (38):

Таким образом, члены ряда (39) либо равны членам сходящегося ряда (38), либо меньше их. Поэтому ряд (39) сходится на основании признака сравнения (см. п. 5, теорему 1 и сноску на стр. 501).

Умножив все члены сходящегося ряда (38) на получим сходящийся ряд

(см. п. 3, теорема 1). Рассмотрим теперь ряд, являющийся разностью сходящихся рядов (39) и (40)

Этот ряд сходится на основании теоремы 2 п. 3.

Но ряд (37) получается из последнего ряда умножением всех его членов на 2:

Следовательно, ряд (37) также сходится (п. 3, теорема 1).

Пример 2. Исследовать на сходимость знакопеременный ряд (33)

Решение. Рассмотрим ряд, составленный из абсолютных величин членов данного ряда

Этот ряд сходится, как обобщенный гармонический ряд с показателем . Следовательно, на основании доказанного признака сходится и данный ряд (33).

Этот признак является достаточным, но не необходимым. Это значит, что существуют знакопеременные ряды, которые сходятся, в то время как ряды, составленные из абсолютных величин их членов, расходятся.

Действительно рассмотрим ряд

который, очевидно, сходится по признаку Лейбница. Между тем, ряд

составленный из абсолютных величин членов данного ряда является гармоническим и, следовательно, расходится.

Хотя рассмотренные выше ряды (33) и (42) оба сходятся, однако характер их сходимости различен.

Ряд (33) сходится одновременно с рядом (41), составленным из абсолютных величин его членов, тогда как ряд (43), составленный из абсолютных величин сходящегося ряда (42), расходится.

В связи с этим введем следующие определения.

Определение. Знакопеременный ряд абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов

На основании достаточного признака сходимости знакопеременного ряда всякий абсолютно сходящийся ряд будет сходящимся.

Определение. Знакопеременный ряд называется неабсолютно сходящимся, если он сходится, а ряд, составленный из абсолютных величин его членов их расходится.

Возвращаясь к рассмотренным выше примерам, можем сказать, что ряд (33) является абсолютно сходящимся, а ряд ( - неабсолютно сходящимся.

Знакопеременными называются ряды, члены которых могут иметь любые знаки, например, .

В частности, если положительные и отрицательные члены ряда следуют друг за другом поочередно, то такой знакопеременный ряд называется знакочередующимся.

Знакочередующие ряды

Знакочередующий ряд, члены которого являются положительными, можно представить в виде

Для исследования сходимости знакочередующихся рядов применяют признак Лейбница.

Признак Лейбница. Знакочередующийся ряд сходится, если абсолютные величины его членов убывают, а общий член стремится к нулю, т. е. если выполняются следующие два условия:

1)
и 2)
.

Достаточно важный класс сходящихся рядов образуют так называемые абсолютно сходящиеся ряды. При этом членами таких рядов могут быть любые действительные числа.

Определение 9.5. Рядназывается абсолютно сходящимся, если сходится
.

Теорема 9.4. Если ряд
сходится, то и рядтоже сходится.

Данная теорема утверждает, что если ряд абсолютно сходится, то он и просто сходится.

Необходимо отметить, что:

1) для знакопостоянных рядов понятие сходимости и абсолютной сходимости совпадают;

2) ряд называется условно сходящимся, если он сходится, а ряд
расходится.

Рассмотрим признаки Даламбера и Коши для произвольных знакопеременных рядов.

Признак Даламбера. Если существует
, то при
рядабсолютно сходится, при
ряд будет расходящимся, при
признак не решает вопроса о сходимости ряда.

Задача 9.7. Исследовать сходимость ряда

Здесь за каждыми двумя положительными членами ряда следует два отрицательных. Для исследования сходимости такого ряда воспользуемся признаком Даламбера.

.

Исходный ряд сходится по признаку Даламбера.

Задача 9.8. Исследовать ряд на абсолютную сходимость

Здесь
. Для такого ряда выполняются следующие условия:

а)

б)
. Следовательно, исходный ряд сходится в соответствии с признаком Лейбница.

Исследуем заданный ряд на абсолютную сходимость. Для этого составим ряд
из абсолютных величин:

Такой ряд представляет собой бесконечно убывающую геометрическую прогрессию, которая всегда сходится. Таким образом, исходный ряд сходится абсолютно.

Задача 9.9 . Исследовать сходимость ряда

Здесь
, следовательно ряд расходящийся, так как не выполняется необходимое условие сходимости.

Тема 9.2. Функциональные ряды

Пусть задана следующая последовательность функций
, т. е.

которая определена на некотором множестве. Если члены такой последовательности соединить знаком плюс, то получают выражение

или
. Такие выражения называют функциональными рядами, а функция
называется общим членом ряда.

Частными суммами ряда
называются функции вида

Функциональный ряд
называется сходящимся при
или в точке (), если в этой точке сходится последовательность его частных сумм:

Другими словами, можно отметить, что функциональный ряд
сходится при
, если сходится числовой ряд
.

Предел последовательности
, обозначим его через
, называется суммой ряда
в точке.

Определение 9.6. Совокупность всех значений, для которых сходится ряд
, называется областью сходимости этого ряда.

Пусть
на отрезке тогда
на рассматриваемом отрезке. В этом случае отмечают, что функция
разлагается в ряд на отрезке
.

Как было показано, сходимость функционального ряда на отрезке
означает, что для любого значенияотрезка
соответствующий числовой ряд сходится. В этой связи для исследования на сходимость функциональных рядов можно использовать признаки сходимости числовых рядов.

Задача 9.10. Найти область сходимости ряда

Компактно этот ряд можно представить следующим образом

.

Этот ряд сходится для всех
. Действительно, для каждого
сумма ряда равна(сумма бесконечно убывающей геометрической прогрессии). Таким образом, в интервале
исходный ряд определяет функцию